搜索二维矩阵 - LeetCode 热题 64

大家好！我是曾续缘🧡

今天是《LeetCode 热题 100》系列

发车第 64 天

二分查找第 2 题

❤️点赞 👍 收藏 ⭐再看，养成习惯

搜索二维矩阵
给你一个满足下述两条属性的 m x n 整数矩阵：

每行中的整数从左到右按非严格递增顺序排列。
每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：
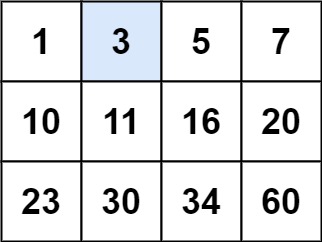输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true
示例 2：
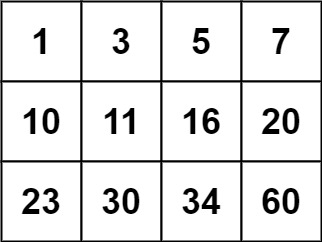输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false
提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-10⁴ <= matrix[i][j], target <= 10⁴
难度：💖💖

解题方法

首先，我们需要明确题目中矩阵的两个特性：每一行从左到右递增，每一行的第一个数比上一行的最后一个数大。这意味着整个矩阵在某种意义上是“排序”的，我们可以利用这一点来快速定位元素。
在解决这个问题时，我们可以把矩阵看作一个一维数组，然后使用二分查找算法。如何把二维矩阵映射到一维数组呢？考虑到矩阵有 m 行 n 列，我们可以将矩阵的行优先展开，即先放置第一行的所有元素，然后是第二行，依此类推。这样，矩阵中的元素 matrix[i][j] 将会映射到一维数组中的位置 i * n + j。
接下来，我们可以在这个假想的一维数组上使用二分查找。二分查找的基本思想是在有序数组中通过重复将搜索区间减半来定位目标值。具体步骤如下：

确定搜索范围的最小和最大索引，初始时最小索引 l 为 0，最大索引 r 为 m * n - 1（即矩阵中最后一个元素的索引）。
计算中间索引 mid = (l + r) / 2，然后找到这个索引对应的矩阵中的元素 matrix[mid / n][mid % n]。
比较这个元素与目标值 target：
- 如果相等，说明找到了目标值，返回 true。
- 如果小于目标值，说明目标值应该位于当前元素的右侧，于是我们将搜索范围的最小索引调整为 mid + 1。
- 如果大于目标值，说明目标值应该位于当前元素的左侧，于是我们将搜索范围的最大索引调整为 mid - 1。
重复步骤 2 和 3，直到找到目标值或者搜索范围为空（即 l > r），此时如果还没有找到目标值，则返回 false。
这个方法的时间复杂度是 O(log(m*n))，空间复杂度是 O(1)，因为我们在原地进行搜索，没有使用额外的空间。

Code

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int l = 0, r = m * n - 1;
        while(l <= r){
            int mid = (l + r) / 2;
            int val = matrix[mid / n][mid % n];
            if(val == target){
                return true;
            }else if(val < target){
                l = mid + 1;
            }else{
                r = mid - 1;
            }
        }
        return false;
    }
}